本帖最后由 季理GiLiGiLi 于 2023-11-7 19:26 编辑
比如,玩家在某个区域内不想进行某一操作,放触发器又要太多太多太麻烦了,可以通过射线检测法,不放触发器就能检测玩家是否在某一个区域内。无论是凸多边形还是凹多边形。
原理:
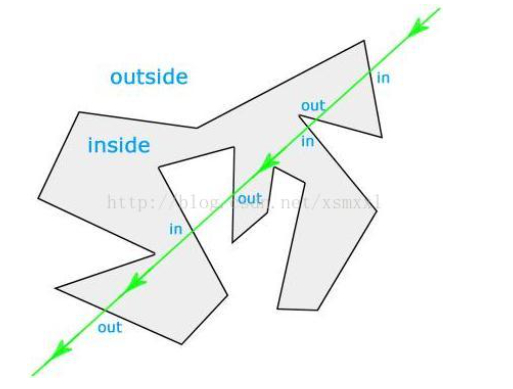
求解从该点向右发出的水平线射线与多边形各边的交点,当交点数为奇数,则在内部。
不过要注意几种特殊情况:1、点在边或者顶点上;2、点在边的延长线上;3、点出发的水平射线与多边形相交在顶点上(很多时候不需要那么准确 所以可以不用考虑特殊情况)
算法思路:
计算多边形每条边的线性函数,然后从玩家位置发出一条射线 检测是否有交点。
/**
* 射线法检测某点是否在一个区域内 适用于任何多边形 数组Polygon为多边形的每个点(可按顺序连点成线 最终化为一个多边形)
*/
public laserCheckInPolygon(actorPos: Type.Vector) {
if (this._nowPolygon == null || undefined) {
return false;
}
let crossings = 0; //越过的射线数量
for (let i = 0; i < this._nowPolygon.length - 1; i++) {
//检测玩家位置是否在该条边的范围内
let condition1 = actorPos.x > this._nowPolygon[i].PosX && actorPos.x < this._nowPolygon[i + 1].PosX;
let condition2 = actorPos.x < this._nowPolygon[i].PosX && actorPos.x > this._nowPolygon[i + 1].PosX;
//计算斜率
let slope = (this._nowPolygon[i + 1].PosY - this._nowPolygon[i].PosY) / (this._nowPolygon[i + 1].PosX - this._nowPolygon[i].PosX);
//检测发出的射线是否有交点
let y = slope * (actorPos.x - this._nowPolygon[i].PosX) + this._nowPolygon[i].PosY;
if ((condition1 || condition2) && y > actorPos.y) {
crossings++;
console.log(`=======通过边${i}-${i + 1}`);
}
}
let idx = this._nowPolygon.length - 1;
let condition1 = actorPos.x > this._nowPolygon[idx].PosX && actorPos.x < this._nowPolygon[0].PosX;
let condition2 = actorPos.x < this._nowPolygon[idx].PosX && actorPos.x > this._nowPolygon[0].PosX;
let slope = (this._nowPolygon[0].PosY - this._nowPolygon[idx].PosY) / (this._nowPolygon[0].PosX - this._nowPolygon[idx].PosX);
let y = slope * (actorPos.x - this._nowPolygon[idx].PosX) + this._nowPolygon[idx].PosY;
if ((condition1 || condition2) && y > actorPos.y) {
crossings++;
console.log(`=======通过边${idx}-${0}`);
}
console.log(`==================射线通过的条数:${crossings}`);
return crossings % 2 != 0;
}
这个polygon数组可以看成就是一个vector数组,可按照数组0·length的顺序将他们连接起来绘制成一个简单封闭图形(边与边不交叉),所以就可以写一个循环,每两个点算一元一次方程,求交点。
这里可以总结为用一个点集构造简单封闭图形。
思路:取x坐标最大的点A(如果最大x坐标的点不止一个,则取Y坐标最小的点),依次计算A点与其余各点的连线与水平线之间夹角的正切值,然后按照正切值排序,依次连接排序后的各点即组成一个简单图形。
原理:其它所有点都在A点的左侧,所有夹角的范围为-Pi/2~Pi/2,y=tanX是个单调递增函数。
/**
* 通过计算正弦值 绘制多边形
*/
drawPolygon() {
let polygon = MapManager.Polygon.filter((cell) => {
return cell.CellObj.getVisibility()
});
polygon = polygon.sort((a, b) => { //按照posX从大到小排序
return b.PosX - a.PosX;
});
/**离得最远的点 */
let farestPoint = polygon[0];
farestPoint.setPrimary();
let cellsMap: [number, number][] = [];
for (let i = 1; i < polygon.length; i++) { //计算每个点与最远的点向量 的正弦值
let Ax = farestPoint.PosX - polygon[i].PosX;
let Ay = farestPoint.PosY - polygon[i].PosY;
let tan;
if (Ax != 0) {
tan = Ay / Ax;
} else {
tan = Infinity;
}
cellsMap.push([i, tan]); //点和正弦值的映射;
}
console.log(`=========cellsMap1:${cellsMap}`);
cellsMap = cellsMap.sort((a, b) => { //按照正弦值 从大到小排
return b[1] - a[1];
});
console.log(`=========cellsMap2:${cellsMap}`);
let newPoly: Cell[] = [];
newPoly.push(farestPoint);
cellsMap.forEach((e) => {
console.log(polygon[e[0]].PosX, polygon[e[0]].PosY);
newPoly.push(polygon[e[0]]);
});
this._nowPolygon = newPoly;
//连点成线
for (let i = 0; i < polygon.length - 1; i++) {
newPoly[i].shootLaser(newPoly[i + 1].Pos);
}
newPoly[polygon.length - 1].shootLaser(newPoly[0].Pos);
}
 AreaCheckStudy.rar
(100.82 KB, 下载次数: 712)
AreaCheckStudy.rar
(100.82 KB, 下载次数: 712)
|